Home

Octree implementation

In this page, I’m going to expose the work done and the results acquired trying to implement a space partitioning system to optimize intersections in a tridimensional space. This project have been done in less than 8 weeks for the class «Engine Algorithms» that I have coursed in my exchange to Saxion Univeristy during 2018. I’m going to show the implementation of an Octree; a data struct that allows segmenting the space to do more manageable the objects that we have in our scene. Also, I’m going to show how the use of different implementations could result in different results.

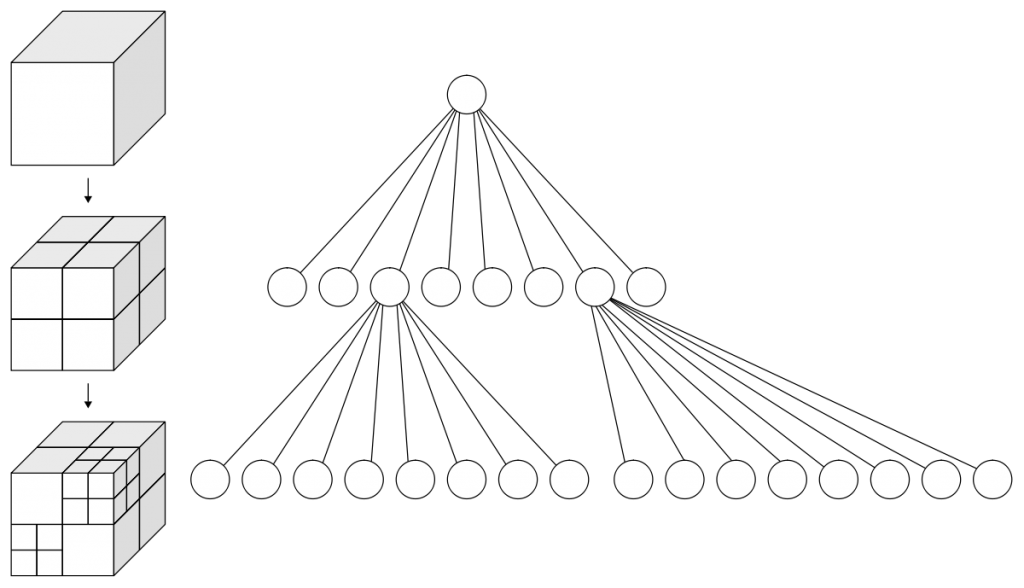
In this case, I’m going to use a static Octree implementation, this means that the Octree structure is going to be defined at the beginning of the execution and It is going to stay invariable until the end of the life of the Octree. Other possibles implementations could be for example define the structure of the Octree(the number of levels for example) depending on the number of objects or the distribution of those elements.

Theoretical background

As I have said an Octree helps us in the task of detecting collisions in a 3D space however the nature of the problem is the same at the end. An Octree is just a way to reduce the number of objects that each «space» has to check but locally each of those regions is going to run in O(n^2). In contraposition to other data structures we can not «balance» our tree and It’s possible to have a really bad equilibrated Octree. Knowing this is important because prepare us for the possible results that we are going to have in the future.

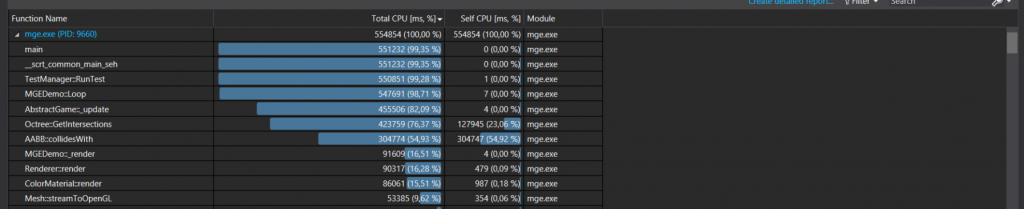
Before starting the project I had one hotspot clear: the function to get the intersections. The data structure of the Octree is, mainly, designed in this case for it so for sure It would take most of the CPU work. As soon as I had a runnable version of the octree I did some CPU work analysis to check the size of the problem.

As we can see in the results the percentage of time used for the function that finds the intersections and the function used to check if there is a collision between two objects took almost the 75% of all the time.   Before going to deeper optimizations (that we are talking later) I decided to polish as much as possible the AABB-AABB collision detection function. Searching on the Internet I found a web page where there’s a one-sentence check where “just need to check that the first AABB’s max point is greater than the second one’s min point and the first one’s min point is less than the second one’s max point” (Miguel Casillas, 2010).

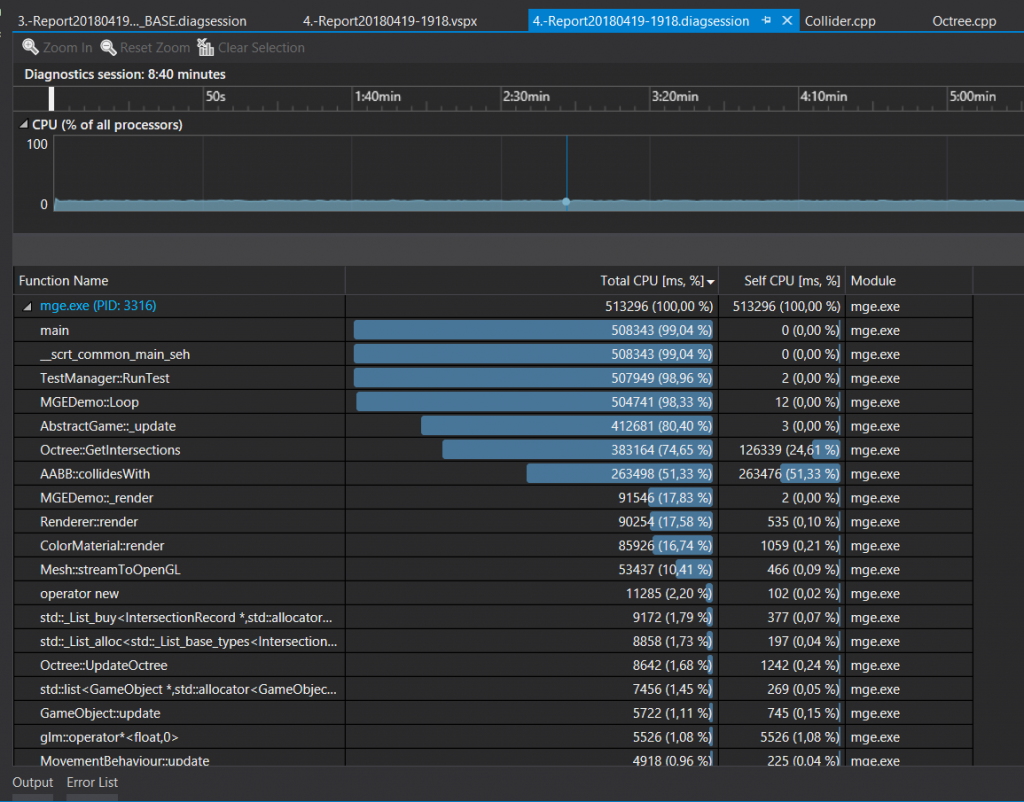
The short-circuit evaluation(the fact that if an evaluation returns false in a sequence of ANDs evaluations the code is going to stop checking the rest of the sentence and it will return false) worked and the cost of the operation was reduced a little more than a 3%.

After some code development, I decided to take some kind of advantage using the fact that some percentage of objects in the scene are statics. I took CPU usages again:

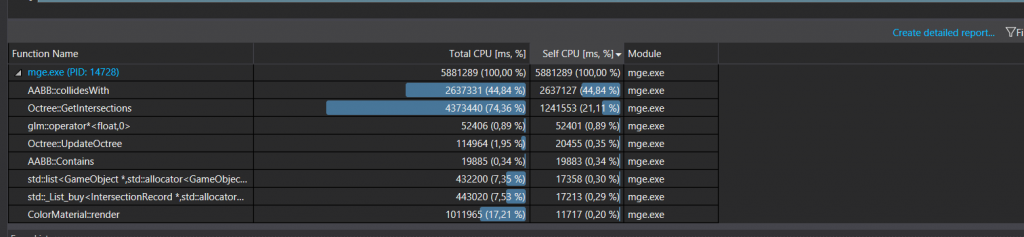
For apply the optimization related to the static objects I use a new list of GameObjects pointers to store the static objects. The collision between this objects is checked once at the beginning of the code execution but after this, they are excluded from the collision tests for local objects in each of the nodes of the Octree(however, they are passed down to the inferior nodes and they are evaluated as all the parent objects).

Furthermore, these static objects are not included in the function function that update the distribution of the objects in the different nodes of the Octree; once they are inserted in one node they are not going to move to another one never.

This optimization reports over a 6% of improvement in the program. It would seem not too much but as we will see in the data analysis section this had a big impact on the performance of the program.

Test setup

For doing the different tests I needed a class responsible of running our demo with different parameters in an automatic way that allow me to disengage of the program during the different runs and last but not least be able to catch all the data generated for the program and write it down in a file.

I coded a class that creates the Octree and the objects to populate the scene changing some parameters as the levels of the Octree or the percentage of static objects in the scene. In addition, this class has come static values to store performance values in real time. The task of writing the data in a file has been done using the library SimpleXlsxWriter allowing me to save all the values in an Excel file for a later analysis if required.

Implementation design ( diagrams ) and coding.

In this section, I’m going to talk about the design of my code and how the different classes are related each other. First, I want to say that (taking into account my situation) I have treated the MGE as kind of «black box» in the sense that I have tried to change the files in it as little as I could. Having this as starting point and after a week trying to figure out how to run the engine, I started codding my Octree class. I followed a tutorial in C# to code a dynamic Octree(Eric Nevala, gamedev.net, 2014); in this Octree the number and depth of the nodes depend on the position and density of the objects in the game region.

This was totally an error because, as I experiment by myself, C# is not C++. This, added to the ignorance of the details of the engine made me have a big mesh after two weeks of work. To solve it I had to «keep it simple» and forget the dynamic implementation. I stopped at that moment to use the tutorial as reference and started to create the structure for my actual code.

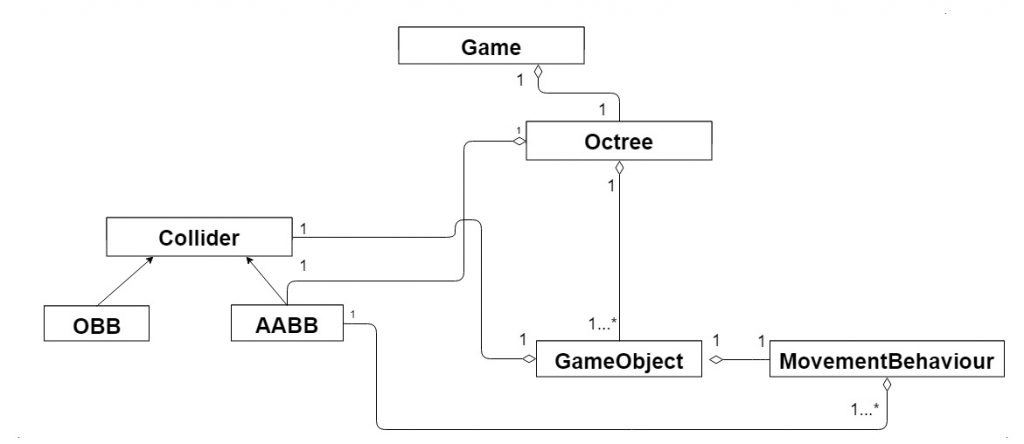
The «game» class(MGEDemo) is on the charge of the update of the different parts of the scene as the hud, the game objects and, of course, the Octree. It contains an Octree reference where the root of our structure is stored. Through this root, all the operations required are called and in this class is processed if needed any possible return value of the Octree.  Two especially important functions in this class are «SetOctree» and «PopulateGame» that are the functions called for our test class to setup the different environments for our tests.

The others class are quite straightforward with the exception of the collision checks in the «Collider» class and the application of the double dispatching technique.  Stopping first on the collision tests, the AABB-AABB just check the maximum and the minimum points of both colliders to know if they are colliding. On the other two cases (OBB-ABB and OBB-OBB) I’m using the Separating Axis Theorem solution. I would like to do some improvements in the case of OBB-AABB due to the fact that knowing the orientation of the AABB axis allow us to delete some dot and cross products (Christer Ericson, Gamedev.net, 2003) but I haven’t have had time enough. The double dispatching technique is related with polymorphism. Thanks to this technique we can avoid knowing if a bounding box is AABB or OBB. Thanks to this, we can generalize code in our Octree class having a Collider* variable for our bounding box.

Data collecting

The collected data try to check if the different implementations help in our interest to achieve the best performance in our program or not. For that, I have chosen the values as main performance references: the fit tests, the time took for 100 iterations and the most important (due to is the main point of work) the number of collisions tests. With this values, we can see if the different implementations in our code are saving checks(the different tests) in our program and in consequence, if we are getting better performance (the FPS). The different values collected depends directly to the different parameters of our run for that those values(as the number of objects in scene, the number of levels of the octree or the percentage of static objects) are stored too.

Data analysis

Here we are going to see that data represented in different charts and what do they mean. Before it I have to say that all the values are normalized to be able to see in the same chart values with really different magnitudes (for example collision tests are measured in millions but the time in our case is sized in the thousands).

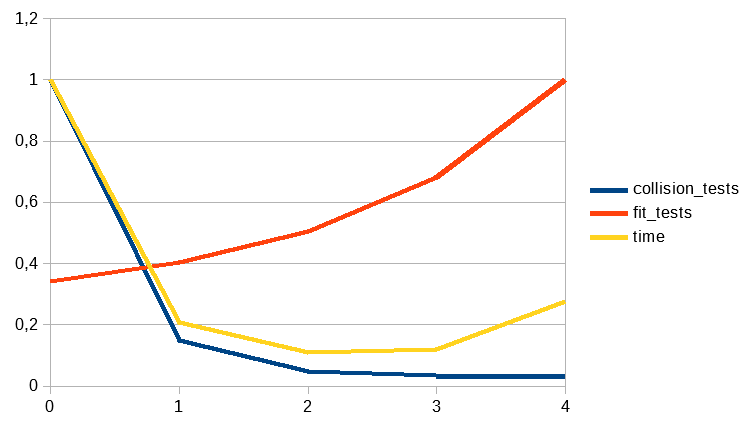
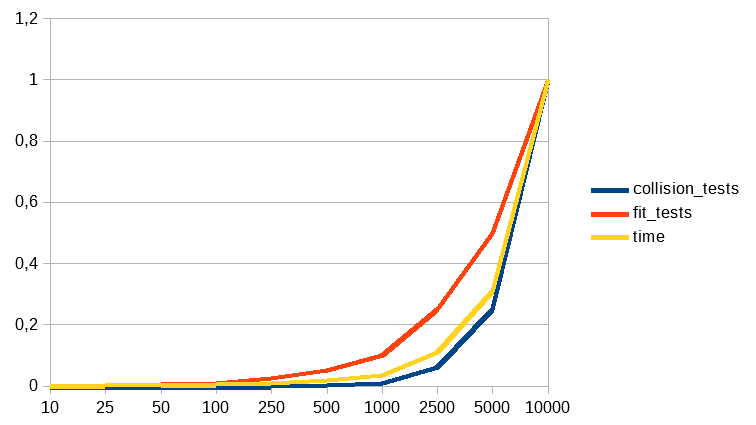
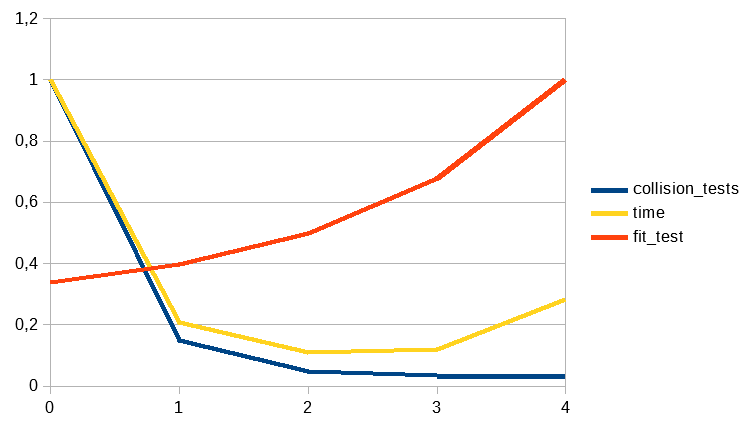
Without static objects implemented – By levels of the Octree – Normalized values
Without static objects implemented – By number of objects – Normalized values

In the second of the images we can see how the Octree presents a complexity value of O(n^2). This result is expected due to the behaviour of the Octree. This data structure is working to reduce the long of N but inside of each of the different sub-N created the complexity still being O(n^2) and, as we know,when we are adding complexities K*O(n^2) is equal to O(n^2). Talking about the first image we can see how the time is really strong linked with the number of collision tests. The number of fit tests affects the time values especially when the Octree get 4  levels of detail and the number of fit tests grows specially fast. The complexity of the collision test seems to be the opposite of an O(log n) so we can extract that the increasing time cost that we can see in the level of detail 4 is due to the number of fit tests and that in the followings levels this tests are continue growing and in consequence increasing the time required.

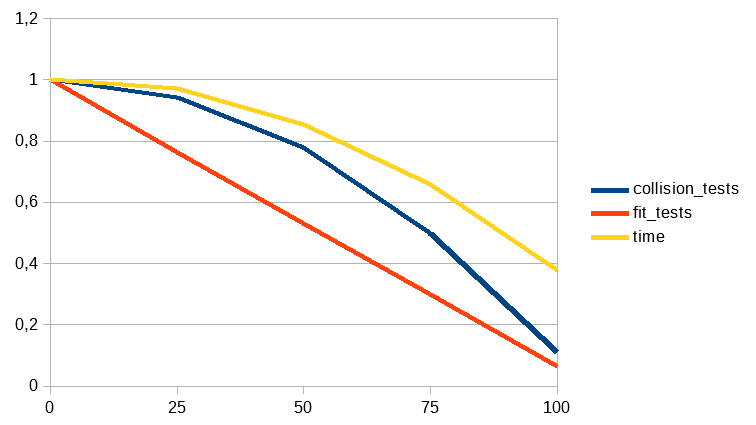
Values by percentage of static objects – Normalized values

Here we can see how our control values change depending of the percentage of static objects in our scene. We can see how the number of fit tests decrease in a linear way but the other two control values are decreasing in a quadratic way.

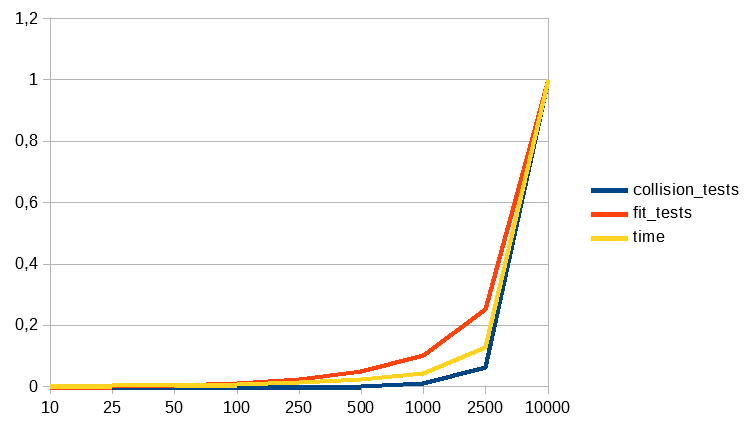
With static objects implemented – By levels of the Octree – Normalized values

With static objects implemented – By number of objects – Normalized values

Is interesting to see how this changes are not affecting to the complexity of our program and that’s clearly reflected in the fact that the shape of the chart that represents the number of tests and the time used to run the program depending of the numbers of levels of the Octree and depending of the number of objects stay practically the same.

As last note I want to add a test done for comparing the time required for do 1 million checks for different colliders:

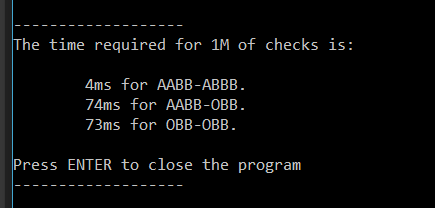
We can see how the AABB-AABB tests is much more faster than the OBB-OBB(or OBB-AABB case)

You can see it working here:  (Tip: Take a look how FPS change depending of the different parameters in the Octree.)

Conclusions

I can extract three big conclusions from the project:

  • Octrees are worth (controlling the number of levels) to control the collisions of a large number of objects in a scene but we are not going to change the complexity of the problem so we have to be careful with the number of objects anyway.
  • Having a good control of the static objects could help to improve the performance
  • Complex colliders add some complexity and probably they are not worth if you don’t need really accurate collision detection.

Resources/References